dΔGr = -ΔSrdT + ΔVrdP
the pressure dependence is:
∂ΔGr / ∂P = ΔVr (1),
where ΔVr is the volume change of the reaction (cm3/mol). Accordingly, the equilibrium constant, log K = - ΔGr / 2.3RT, changes with pressure as:
For example, for dissolution of anhydrite,
CaSO4 = Ca+2 + SO4-2
the molar volumes (at 25oC, I = 0) are:
CaSO4: 46.1 cm3/mol, Ca+2: -18.2 cm3/mol, SO4-2: 14.4 cm3/mol.
For dissolution of anhydrite, ΔVr = -18.2 + 14.4 - 46.1 = -50 cm3/mol. The equilibrium constant at 500 atm (equivalent to 5000 m depth) can be calculated with eqn (2):
Thus, K at 500 atm is 100.44 = 2.8 times higher than at 1 atm. The solubility of anhydrite increases by √2.8 = 1.7.
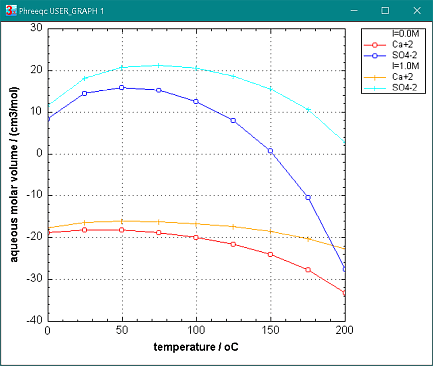
Aqueous volumes of solute species are defined by convention relative to the volume of H+ = 0 cm3/mol. The aqueous volume of Ca+2 can be negative, because the density of a CaSO4 solution, relative to an equimolar H2SO4-solution, increases more than is given by replacing 2 H+ (2 g/mol) by 1 Ca+2 (40 g/mol). Thus, Ca+2 appears to have a smaller volume in water than H+, but that is because the density difference is wholly attributed to Ca+2. Physically, the density change is due to compaction of water molecules around Ca+2 by electrostatic attraction of the dipoles on H2O to the ion.
The charge on the water dipoles is a function of the dielectric permittivity. If the dielectric permittivity decreases by temperature increase, more water molecules are needed for compensating the charge on the ion, and the apparent volume becomes smaller of most ions. (Actually, the volume change follows from the pressure derivative of the Born equation, like in eqn (1), as explained in aqueous molar volumes .)
The effect of temperature on the molar volumes of Ca+2 and SO4-2 is illustrated in the figure (PHREEQC input file Vm_Ca_SO4.phr).