MULTICOMPONENT DIFFUSION IN CLAYS

Diffusion in clays depends on a number of factors. Solutes have different diffusion coefficients. Anions are excluded from the diffuse double layer (DDL), and thus diffuse over a smaller surface area than cations and neutral species. Cations accumulate in the DDL or are sorbed, which endows them with higher concentration gradients than other species.
Let's do model experiments to illustrate the effects following Appelo and Wersin, 2007. Two cores are taken from Opalinus Clay and contacted for 1 year with a boundary solution made of porewater to which tritium (HTO), I- and 22Na+ are added as tracers. The concentrations of the tracers in the boundary solution decrease as they diffuse into the core, and we want to see how that depends on the properties of the tracers and the clay. PHREEQC's transport option -stagnant is used to compute the concentrations in the boundary solution.

First, 'classic' PHREEQC and multicomponent diffusion (MCD) are compared, with all solutes having the same tracer diffusion coefficient of HTO (2.24*10-9 m2 / s). The concentrations diminish by diffusion in the sediment. The results are identical for the 3 tracers with the 2 model options (PHREEQC input file opa_col0.phr):

Next, multicomponent diffusion (MCD) is calculated, with each solute having its own tracer diffusion coefficient.
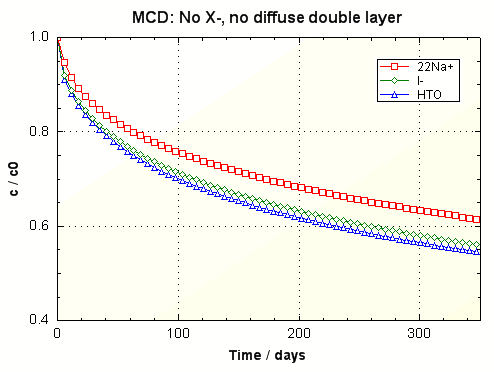
The first core contains no clay and has neither DDL nor sorption capacity (for this example). The figure shows the decrease of the tracer concentrations with time in the outer solution (PHREEQC input file opa_col1.phr). HTO declines faster than I-, which in turn decreases quicker than 22Na+. This is in agreement with the order of the tracer diffusion coefficients, HTO > I- > 22Na+ (listed in phreeqc.dat).

The 2nd core has the same porosity, but it contains montmorillonite with an exchange capacity of 1.6 eq/L, compensated by counter ions in the DDL. Half of the pores is occupied by the DDL from which I - is excluded completely with option '-only_counter true'. As a result, the accessible surface for I- is smaller, and this anion disappears slower than in the previous case. 22Na+ accumulates in the DDL, therefore the concentration in the free pore solution is initially smaller than of anions and neutral species. Consequently, the concentration gradient is higher and 22Na+ diffuses faster than in the former case (PHREEQC also calculates the diffusion in the DDL with option -Donnan of keyword SURFACE). The decrease of HTO is the same in all cases. (PHREEQC input file opa_col2.phr)


New diffusion experiments have shown that equal-charged tracers are enriched (or depleted) differently in the DDL, probably because of increased complexation as a result of the decreased dielectric permittivity of water close to a charged surface (Appelo, Van Loon and Wersin, 2010). Furthermore, surface or interlayer diffusion can be significant for very strongly sorbed cations such as Cs+. For modeling these effects, PHREEQC 2.16 has been extended with option '-erm_ddl' (for enrichment in the DDL), and option '-interlayer_d' in TRANSPORT (for diffusion of exchangeable cations).
As an illustration, the 2nd core is modeled by distributing the exchange capacity over interlayer sites X - = 0.96 eq/L and counter ions in the DDL = 0.64 eq/L (40% of the CEC). Furthermore, Cl - and Cs+ are added as tracers (PHREEQC input file opa_col3.phr).
The DDL enrichments for Cl- and I- are set to 0.6 and 0.3, respectively (SOLUTION_SPECIES). Thus, I- is more depleted than Cl- and will diffuse less than Cl-, even if both anions have the same diffusion coefficient. The anion exclusion from the DDL shows up in an increased tortuosity factor: when DDL's overlap in pore constrictions, anions are forced to circumnavigate the obstruction, while HTO and cations can still pass. The higher tortuosity can be modeled by introducing additional diffusional paths that are inaccessible for anions or by lowering the free water diffusion coefficient (-dw in SOLUTION_SPECIES).
The different effects of interlayer diffusion for Na+ and Cs+ are evident in the graph. Because the cation-exchange selectivity for Cs+ is very high (100 times higher than for Na+), more than 99% of Cs+ resides in the interlayer domain. If interlayer diffusion is set to 'false' in the second simulation, Cs+ disappears notably slower, while the concentration trend of Na+ is very little affected. The concentration profiles of HTO and the anions remain the same (this depends on the fraction of water that is assigned to the interlayers).

In the files, option -stagnant of keyword TRANSPORT is used to calculate diffusion over the interfaces of the cells. This enables to model concentration changes in the boundary solution. Mixing factors are calculated with Eqn (128) of the PHREEQC-2 manual (p. 52) for the physical dimensions given in the table below. ε is the porosity, θ2 is the tortuosity-factor, VH2O is the volume of water in a cell, and V0 is the volume of the external solution with tracers in contact with the clay.

-- For classic PHREEQC, the mixing factors are calculated with the cell volumes, as explained with Eqn (128) in the PHREEQC-2 manual (p. 52).
-- For multicomponent diffusion, the mixing factors must be calculated with a volume of 0.001 m3, and the actual volume of water in a cell is entered when the SOLUTION is defined. The diffusion coefficient and porosity that were used for the mixing factors must be entered with option -multi_D in the input file. PHREEQC adapts the mixing factor for individual solutes by the ratio of the tracer diffusion coefficient and the default diffusion coefficient given with -multi_D. For each cell, only mixing factors with higher numbered cells need be entered. If PHREEQC warns that concentrations turn negative, the mixing factor must be reduced, which is generally possible by letting PHREEQC take time-substeps:
-time 5e5 3 # 5e5 seconds are substepped into 5e5 / 3 = 1.666e5 sec.
Three more examples illustrate how option stagnant can be used:
  • Input file ddl_flux.phr calculates steady state diffusion through the DDL.
  • Input file il_flux.phr does the same through the interlayer space.
  • Input file stagnant_multiD.phr calculates advective transport of tetra with mixing into a sorbing clay layer (Table 10.3 in Appelo and Postma, p. 508).
    • In the first 2 cases, the standard column and the stagnant results are compared with the analytical solution. The 3rd example shows how transport of tetra can be calculated with option multi_d true, and with options:
    -multi_d false; -stagnant 1 1.55e-9 0.24 0.12 # 1 stagnant layer, alpha, mobile por, immobile por.

    References
    Appelo, C.A.J. and Wersin, P., 2007. Multicomponent diffusion modeling in clay systems with application to the diffusion of tritium, iodide and sodium in Opalinus Clay. Env. Sci. Technol., 41, 5002-5007.
    Appelo, C.A.J., Van Loon, L.R. and Wersin, P., 2010. Multicomponent diffusion of a suite of tracers (HTO, Cl, Br, I, Na, Sr, Cs) in a single sample of Opalinus Clay. Geochim. Cosmochim. Acta 74, 1201-1219.

    «—