PHREEQC 3.8 comes with a new database, PHREEQC_RATES.DAT, which has kinetic rate parameters in a tabular format for a plethora of minerals, copied directly from the compilations by Palandri and Kharaka (2004), Sverdrup et al. (2019) and Hermanská et al. (2022, 2023). The database is used to calculate the rates as a function pH and temperature, and possibly other variables, for example the concentration of a specific solute. It is no longer necessary to write a detailed BASIC program for these rates, which greatly facilitates to intercompare the various rates in a kinetic model.
Kinetic rates are derived from the moles of mineral that reacts with time in an experiment:
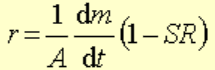
where r is the rate (mol/m2/s), A is the surface area of the mineral, m is moles of mineral, t is time, and SR the saturation ratio. The factor (1 - SR) is the affinity that lets the rate go to zero when the solution is in equilibrium with the mineral.
The rates are a complex function of the concentrations of protons, hydroxyls, and other ions, and of course, of temperature and pressure. For example, the pH dependence of Na- and K-feldspar dissolution rates shown in Figure 1a indicates that the rate is smallest at neutral pH and increases towards lower and higher pH. We can imagine that it is related to protons entering the mineral at low pH, displacing the metal ions, and to detachment of the structural [Al,Si3]O8 tetrahedra into solute complexes Al(OH)4- and H3SiO4- at high pH. To describe this behavior, the equation for the rate must have the form:
where k and n are coefficients that may depend on temperature, pressure and other solutes, and the brackets indicate activities of the protons and the hydroxyl ions.
How is the surface area of the mineral defined? It can be estimated assuming that the mineral grains are spheres or cubes with a smooth surface (Ageom), or by measurement with gas adsorption (ABET). Generally, the measured surface is larger than calculated, since grinding increases the surface roughness λ:
The surface roughness also increases with time because crystal defects and the more soluble members of twins and zoned crystals tend to dissolve faster, creating pits and dissolution valleys. Figure 1b illustrates the appearance of solution valleys in an etching experiment with an albite/orthoclase twin in which albite (NaAlSi3O8) dissolved faster than orthoclase (KAlSi3O8), in agreement with Figure 1a. Figure 1c shows that the surface roughness of freshly ground minerals is about 10, and that it can increase to over 500 in 1 Ma. Clearly, the surface area is an uncertain factor and its definition requires some expertise or local knowledge for field application.
Figure 1. (a) The measured dissolution rate of albite- and orthoclase-feldspars as a function of pH and temperature (Hermanská et al., 2022);
(b) solution valleys developing in albite/orthoclase twins (Lee et al., 1998);
(c) surface roughness of primary minerals in soils as a function of soil age, and of freshly ground minerals with error bars on the left (White and Brantley, 2003).
So, what is needed in a general model for calculating the dissolution rate of a mineral is the specific surface area, the roughness, a parameter that allows to modify the affinity, and the numbers that define the rate as a function of the physical and chemical conditions. For example, the dissolution of albite with the numbers from Hermanská et al. (2022):
RATE_PARAMETERS_HERMANSKA # Acid mechanism Neutral mechanism Basic mechanism # logk25 Aa Eaa n(H+) logk25 Ab Eab logk25 Ac Eac n(OH) ================================================================================================= Albite -10.32 0.7 58 0.3 -11.19 0.21 60 -13.58 1.50E-05 50 -0.3The rate is invoked with RATE_HERMANSKA("Albite") in a RATES block:
RATES
Albite_Hermanska # rate name, called in KINETICS
5 REM PARMS: 1 affinity, 2 m^2/mol, 3 roughness, 4 exponent for (m/m0)
10 if parm(1) = 1 then affinity = 1 else affinity = 1 - SR("Albite") : if affinity < parm(1) then SAVE 0 : END
20 rate = RATE_HERMANSKA("Albite")
30 IF M > 0 THEN area = M * parm(2) * parm(3) * (M/M0)^parm(4) ELSE area = 0
40 SAVE area * rate * affinity * TIME
-end
The rate is called in a KINETICS block that also defines the 'parms':
KINETICS 1 Albite_Hermanska; -formula NaAlSi3O8 -parms 0 1 1 0.67 END
The KINETICS block starts with the rate name Albite_Hermanska, and the formula of the mineral since the rate name is different from the name 'Albite' in PHASES in PHREEQC_RATES.DAT. The four 'parms' give the affinity factor, the specific surface area (m2 / mol), the surface roughness, and the exponent for m/m0, respectively.
The PHREEQC file rates_comp.phr calculates kinetic reactions for albite, calcite, quartz and montmorillonite shown in figures 2-5.
|
Figure 2. Initial rates of albite dissolution as a function of pH at 25oC. The circles are measured rates from Chou and Wollast (1985), the red line gives the rate according to Palandri and Kharaka (2004), the green and blue lines result from the compilations of Sverdrup et al. (2019) and Sverdrup and Warfvinge (1995), and the yellow line is from Hermanská and follows the blue dashed line in figure 1a.
RATE_PARAMETERS_PK # Acid Neutral Base # log K E n(H+) log K E log K E n(OH-) # ========================================================= Albite -10.16 65 0.317 -12.56 65 -15.6 66.5 -0.471 # PK, Table 1 Albite -10.9 0 0.5 -13.3 0 -16.0 0 -0.3 # Sverdrup, 25şC Albite -10.32 58 0.3 -11.19 60 -13.58 50 -0.3 # Hermanská # In figure 2, the Sverdrup rates are calculated with a surface rougness of 20 |
|
|
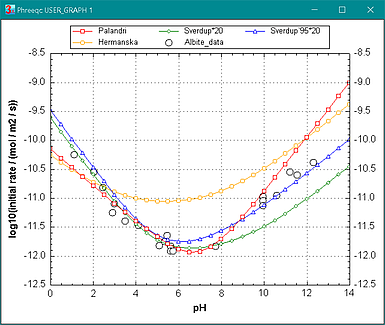
Figure 3. Calcite dissolution in pure water with initial PCO2 = 10-2.5 and 10-1.5 at 25oC, calculated with the rates of Palandri and Kharaka (2004) and of Plummer et al. (1978). The calculated concentrations of Palandri and Kharaka are consistently higher than of Plummer et al. If the numbers of Plummer et al. are rewritten and entered in the RATE_PARAMETERS_PK block for 25şC, it is apparent that log K for P_CO2 is higher in PK. Palandri uses the CO2 pressure as the parameter for the corresponding rate number, and took Plummer's number. However, Plummer used the aqueous CO2 concentration as parameter, and the number must be decreased by the log of the ratio PCO2 / [CO2]aq = 101.48 at 25şC to calculate the rate correctly with RATE_PARAMETERS_PK.
RATE_PARAMETERS_PK # Acid Neutral P_CO2 # log K E n(H+) log K E log K E n(P_CO2) Table # ================================================================== calcite -0.3 14.4 1 -5.81 23.5 -3.48 35.4 1 33 # PK calcite -0.29 0 1 -5.92 0 -4.96 0 1 33 # PWP, 25şC # The PWP numbers are multiplied with 10, to go from mmol to mol in solution (divide by 1e3), and from cm2 to m2 for the surface area of calcite (multiply witn 1e4). Furthermore, log K for P_CO2 is decreased by 1.48. |
|
|
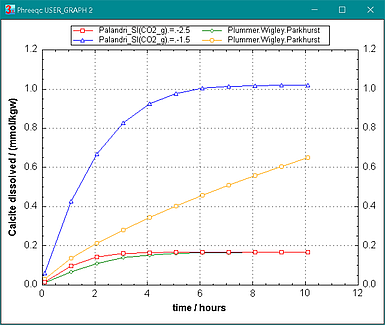
Figure 4. Kinetic quartz dissolution in pure water at 25şC according to the rate parameters in PHREEQC_RATES.DAT, and by Rimstidt and coworkers. The surface area is 6 m2/ mol, representative for water in a soil. The Na-effect in the Rimstidt rates is calculated for a 1 mM NaCl solution, but is not considered in the other rates.
RATE_PARAMETERS_PK
# Acid Neutral Base
# log K E n(H+) log K E log K E n(OH-) # Na-factor
# =========================================================
Quartz -30 0 0 -13.4 90.9 -30 0 0 # --, PK
Quartz -14.6 0 0.3 -13.8 0 -14.7 0 -0.3 # --, Sverdrup, 25şC
Quartz -11.4 45.6 0.3 -30 0 -15 80 -0.4 # --, Hermanská
Quartz -30 0 0 -13.3 90 -30 0 0 # 1500 * tot("Na"), Dove and Rimstidt, 1994
# 5e-5 * act("Na+")^0.3 * act("OH-")^0.4, Rimstidt, 2015
|
|
|
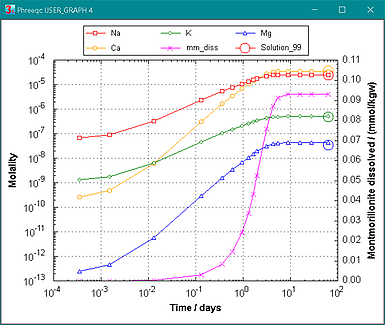
Figure 5. Kinetic dissolution of montmorillonite with initially equal equivalents of exchangeable Na+, K+, Mg2+ and Ca2+. The exchange reaction is much faster than the dissolution reaction. Thus, when the cations are released by dissolution of the kinetically dissolving TOT layer, the solute concentrations change in relation to the solution composition and the exchange constants.
0.34 K+ + Na0.34X_montm_mg = K0.34X_montm_mg + 0.34 Na+; log_k 0.58 which gives: log KK\Na = 0.58 / 0.34 = 1.7,
The circles from Solution_99 in figure 5 are the concentrations in equilibrium with the montmorillonite. The file rates_comp.phr also shows how the Gaines Thomas formula for the exchange reaction can be used, and how the default X exchanger can be invoked. |
|
The file kinetic_rates.dat has BASIC programs in which the rates for the three RATE_PARAMETERS_ blocks are calculated. The file is used in kinetic_rates.phr to calculate the inital rates for albite shown in figure 2 (perhaps modify INCLUDE$ c:\phreeqc\database\kinetic_rates.dat to the correct location). The 2 files can be a template for modifying or adding rate parameters.
References
Bruggenwert, M.G.M. and Kamphorst, A., 1982. Survey of experimental information on cation exchange in soil systems. in: G.H. Bolt, ed., Soil chemistry B. Physico-chemical models, Chpt. 5. Elsevier.
Chou, L. and Wollast, R., 1985. Steady-state kinetics and dissolution mechanisms of albite. Am. J. Sci. 285, 963-993.
Dove, P.M. and Rimstidt, J.D., 1994. Silica-water interactions. Rev. Mineral. Geochem., 29(1), 259-308.
Hermanská, M., Voigt, M.J., Marieni, C., Declercq, J. and Oelkers, E.H., 2022. A comprehensive and internally consistent mineral dissolution rate database: Part I: Primary silicate minerals and glasses. Chem. Geol., 597, p.120807
Hermanská, M., Voigt, M.J., Marieni, C., Declercq, J. and Oelkers, E.H., 2023. A comprehensive and consistent mineral dissolution rate database: Part II: Secondary silicate minerals. Chem. Geol., p.121632.
Lee, M.R., Hodson, M.E. and Parsons, I., 1998. The role of intragranular microtextures and microstructures in chemical and mechanical weathering: direct comparisons of experimentally and naturally weathered alkali feldspars. Geochim. Cosmochim. Acta 62, 2771-2788. And pers. comm.
Palandri, J.L. and Kharaka, J.K., 2004. A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling. USGS Open-File Report 2004-1068, 71 p.
Plummer, L.N., Wigley, T.M. and Parkhurst, D.L., 1978. The kinetics of calcite dissolution in CO 2-water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO 2. Am. J. Sci., 278(2), pp.179-216.
Rimstidt, J.D., 2015. Rate equations for sodiumcatalyzed quartz dissolution. Geochim. Cosmochim. Acta 167, 195-204.
Sverdrup, H. and Warfvinge, P., 1995. Estimating field weathering rates using laboratory kinetics. Rev. Mineral. Geochem. 31, 485-541.
Sverdrup, H., Oelkers, E., Erlandsson Lampa, M., Belyazid, S., Kurz, D. and Akselsson, C., 2019. Reviews and syntheses: Weathering of silicate minerals in soils and watersheds: Parameterization of the weathering kinetics module in the PROFILE and ForSAFE models. Biogeosciences Discuss. 1-58.
White, A.F. and Brantley, S.L., 2003. The effect of time on the weathering of silicate minerals: why do weathering rates differ in the laboratory and field? Chem. Geol. 202, 479-506.